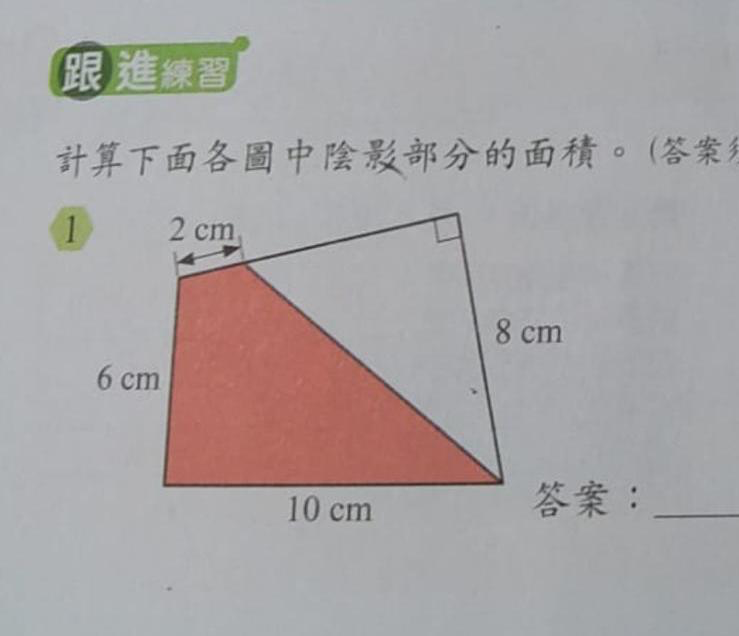
Question 1
分享自 LIHKG 討論區 – https://lih.kg/bNHpxT
很多人做數的時候,都會產生一種奇怪的錯覺。
即使問題出得多麼含糊,只要有足夠的智慧和耐性,人人都會找到一個唯一,絕對的正確答案。
Wrong Answer A
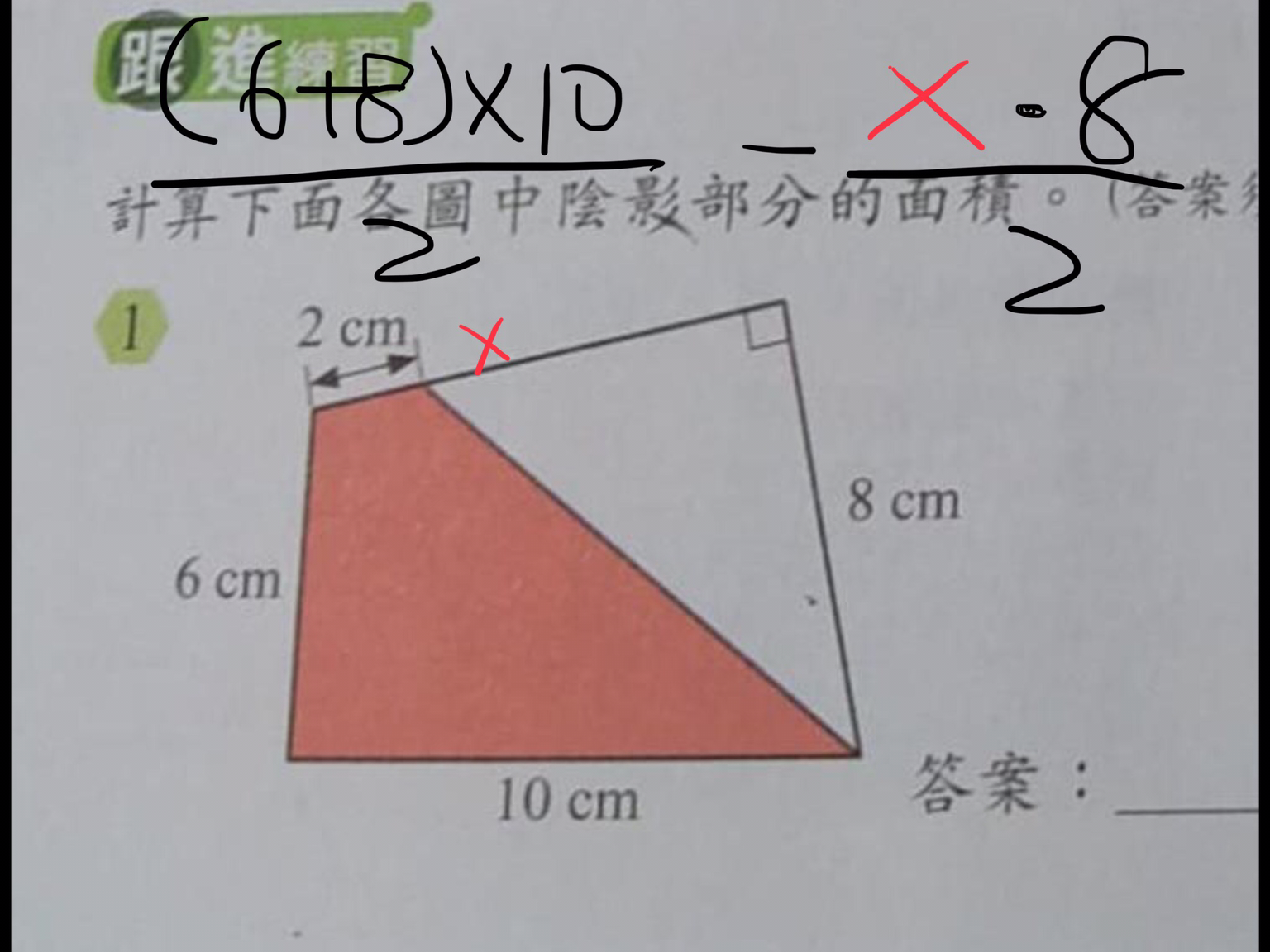
評語:沒有梯形的話,請不要用梯形的 formula。
Wrong Answer B
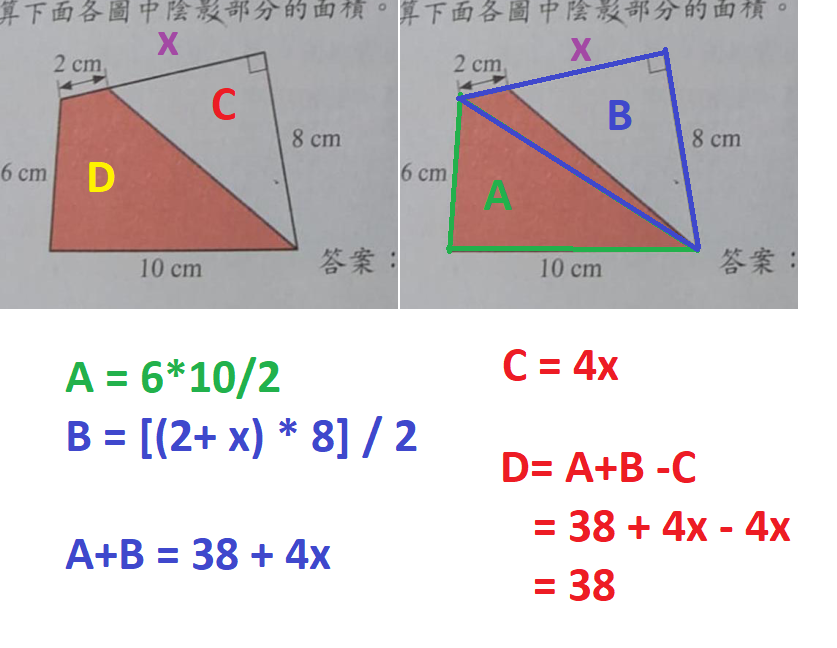
評語: A 未必是直角三角形。請再接再厲。
Wrong Answer C
成班都 on9
#161 – https://lih.kg/fPptbiX
用間尺度返個實際長度
計個比例出黎
陰影𠝹兩個三角形出黎
用間尺度返個高
計兩個三角形面積相加咪陰影面積囉
成班弱智
評語: 出題者未必按比例畫畫。即使作者按比例畫出圖形,尺子也不能準確地量度出距離和面積。
Correct Answer…?
試想像自己在倫敦街頭拿著東京的地圖。即使你怎樣努力去看,也沒可能靠著地圖找到 London Eye 的位置。地圖自身並沒有足夠的線索。
學會質疑自己的地圖,才能發現問題所在。

補正一下的話,這條問題的確是有解的。大家有興趣的話不妨試一下。
Question 2

如果 是直角的話,陰影面積是多少?(小學程度)
Question 3

如果 ,陰影面積又是多少?(DSE 程度)
Answer for Q2

Answer for Q3

By Pythagorean theorem,
Applying Heron’s formula,
where . Hence,
Putting everything together:
小故事
「陳老師,我有嘢唔明呀…」
小明拿着自己的試卷,走到老師的桌前。
「呢條題目嘅答案,唔係咪 38 咩?我計錯咗 D 咩呀?」
小明昨日用了數小時重計了這題。然而,他沒有計出其他答案。
問了幾個師兄和連登上的巴打,也找不出錯處。
這樣一來,錯的只可能是陳 Sir 了。
「來吧,讓我看看你尷尬的表情…」小明心中偷笑着。
「呢條數,你冇計錯到呀。」
「吓!?噉做咩冇分嘅?」
「因為答案唔係 38,而係 。」
小明看一看試題,的確每條邊都標着 cm。
恐怕連登上的巴打也沒有注意到吧。
「但係,至少可以畀我半分嗎?」
「不了…小明,你唔記得喇咩?喺我嘅考試裏面,只有全對先有分。」
「…」
「教不嚴,師之惰呀。重有乜嘢問題?」
輸了。
「冇喇。唔該陳老師。」小明垂頭喪氣地離開教員室。
陳 Sir 拿着自己的咖啡杯,掩蓋自己暗中揚起的嘴角。
給半分,合情,但不合理。
要是甚麼都給 effort 分的話,我豈能建立那美好的 bell curve?
喝下那褐色的液體,陳 Sir 的心情又暢快了起來。
今天的咖啡,份外香醇呢。
